Tyrannosaurus

Hutchinson, John R. & Garcia, Mariano, 2002, Tyrannosaurus was not a fast runner, Nature 415 (28), pp. 1018-1021 : 1018-1021

Most assessments of running ability in large theropods are qualitative, based on analogies to walking elephants or running birds and hoofed mammals 3,5–7. Earlier quantitative assessments of the biomechanics of Tyrannosaurus suggested that it had limited locomotor performance 1, 2, 4, 8, 9, but uncertainties about tyrannosaur anatomy, physiology, and behaviour have impeded resolution of this debate 1 – 9. Fossilized footprints demonstrate that smaller theropod dinosaurs could run 10, but running tracks from large theropods are unknown 7, 9. Bulky limbs and other analogies with elephants provide evidence that the enormous sauropod dinosaurs did not run 1, 2, 5, 11.

For extant animals, our results ( Table 1 ) matched reality: alligators cannot run bipedally, whereas chickens are adept runners. Our dissected Alligator only had about 3.6% m body per leg as extensor muscles, but we estimated that it would need about 7.7% m body per leg to run quickly on its hindlimbs. In contrast, our Gallus specimen had about 8.8% m body per leg as extensor muscles, but it should only need about 4.7% m body per leg for fast running. Thus alligators have less than half the extensor muscle they would need to run fast, whereas chickens have almost twice the required amount of extensor muscle.

Well known scaling principles 12 – 14 predict that animals of larger body mass (m body) have more restricted locomotor performance because muscle force scales as (m body) 0.67, whereas muscle mass scales as (m body) 1.0. To be a fast runner, a Tyrannosaurus would have needed enough extensor muscle mass to support itself. We calculated ( Fig. 1 ; Methods) this mass for various animals to determine whether running would require too much muscle mass.

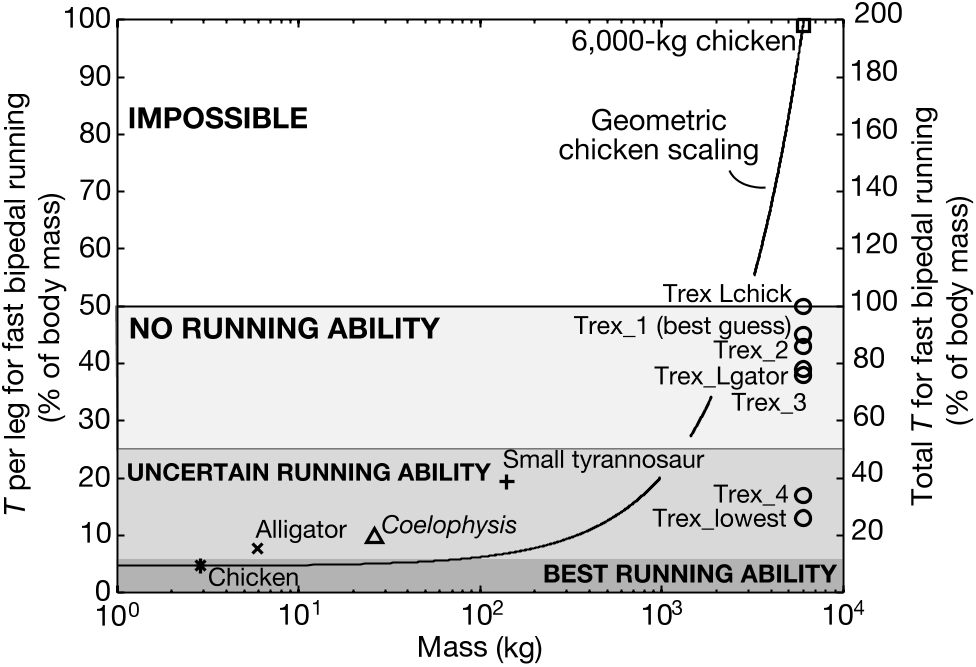
Smaller theropods had lower estimates of minimum extensor muscle mass per leg (T) than Tyrannosaurus ( Table 1 ), and thus we expect they had a broader range of running performance. We initially calculated ( Fig. 2 ) that Tyrannosaurus needed about 43% of its body mass as extensor muscles in each leg (86% m body for both legs) in order to run quickly. This high estimate of T is surprising because our input parameter values were generously weighted towards a low T. These findings suggest that Tyrannosaurus could not run quickly.

A parameter study was then performed to assess the sensitivity of these findings to the values of the assumed parameters. Many of the parameters needed to model the limb mechanics of extinct dinosaurs are uncertain. To test how T was affected by the initial parameters, we entered a range of values and observed how T changed ( Table 2 ). Some unknown parameters, such as the muscle fibre pennation angle (v), were relatively unimportant: within a reasonable range of values (compared to extant taxa) they had little or no effect. Likewise, our approximations of the muscle moment arms (r) were presumably reliable because we used rigorous muscle reconstructions that minimize speculation 15, 16. Although m body is unknown for extinct taxa, our calculation expressed the required extensor muscle mass as a percentage of body mass (T), factoring out m body (see Methods).

In contrast, uncertainty about other parameter values was quite important. The limb orientation used ( Figs 1 and 2 ) was a critical assumption because a more columnar (straight­legged) orientation ( Table 2 ) decreased the moment arms (R) of the ground reaction force (GRF) and hence decreased T compared to a more crouched (bent­legged) limb orientation. A more posterior position of the trunk centre of mass, shorter extensor muscle fibre lengths (L), greater extensor muscle moment arms (r), or a lower multiplier (G) of the GRF would also decrease our estimated values of T ( Table 2 ). The relative lengths of muscle fibres (L) vary widely in extant taxa 17, 18, so this parameter deserves more study. Admittedly, our calculations omitted other parameters that a more realistic model could include (Supplementary Information). However, most of these assumptions were conservative, leading to an underestimate of T.

We asked how much hindlimb muscle mass would be unreasonable for an extinct theropod dinosaur: in extant tetrapods, 50% or less of m body is typically composed of muscle 19. This proportion is independent of m body (ref. 20). Of that 50%, a total of 5–40% of m body is allocated to limb extensor muscles 15,17–19. Considering these data, the simplest inference is that if T is greater than 25% m body per leg as limb extensors (that is, more than 50% m body), a biped could not run quickly (if at all), because it would not have enough muscle to exert the necessary forces.

Judging from extant taxa, values of T from 5–25% per leg indicate that an animal may or may not be a fast runner, depending on the ratio of the actual percentage of m body that is extensor muscle to T, the estimated percentage of extensor muscle required. Values of T closer to 25% probably indicate poor running ability (if any) because the ratio of actual extensor muscle percentage to T would be perilously close to 1. Adept runners (such as ground birds 12, 21) have T values below 5%, maintaining a high ratio of actual extensor muscle mass to T (almost 2.0 in Gallus ). This allows the musculoskeletal system to operate with a generous margin of safety 12 – 14 to accommodate unexpected increases of joint moments.

Some robust conclusions are possible despite the uncertainties about parameter values. Our findings agree with data from fossilized footprints (fastest estimated speeds are, 11 m s ­1) 9, 10 indicating that smaller theropods could run quickly. Although our T estimates are somewhat high (10–21% m body per leg), a more columnar limb orientation could easily have reduced T enough to enable fast running (,5% m body).

Yet our estimates of T for an adult Tyrannosaurus were so high that it is difficult to justify the reconstruction of Tyrannosaurus as a fast runner. Even with generous assumptions we were unable to reduce the estimates of T to 5% m body per leg or less. Indeed, scaling data 17, 18 suggest that a 6,000 kg Tyrannosaurus had only 7–10% m body per leg as extensors. Therefore we conclude that an adult Tyrannosaurus had very limited, if any, running ability. Our best estimates indicate that an adult Tyrannosaurus needed over 40% m body per leg as extensor muscle. If this is correct, then such animals were unable to run at all. If Tyrannosaurus was indeed an adept runner, then it must have had many musculoskeletal specializations that available data do not suggest.

A final model is illustrative. We isometrically scaled­up our chicken model to 6,000 kg to simulate a Tyrannosaurus ­sized chicken. Our model shows that a gigantic chicken, using the same limb orientation as an extant galliform 21, would need 99% m body per leg as extensor muscles to run quickly, which is clearly impossible and is much higher than for a typical chicken (4.7% m body per leg). Features such as the more posterior position of the trunk centre of mass of Tyrannosaurus explain why we obtained lower estimates of T for Tyrannosaurus (43% m body per leg) than for the 6,000 kg chicken. Nonetheless, the high estimated values of T in both models reveal how giant terrestrial animals become restricted from extreme locomotor performance 9, 13.

The ‘giant chicken’ example naturally prompts one to look at equation (1) in terms of scaling. Assuming isometric scaling, and that muscle pennation (v) and stress (j) are independent of body mass 13, 17, 18, 22, we predict that T increases linearly with increasing size ( Fig. 3 ). We expect T to increase with mass roughly in the manner shown by the dashed curve in Fig. 3 , especially if limb orientation remains quite flexed.

Our conclusions lead us to question the reconstructions of Tyrannosaurus running at 11–20 m s ­1 (refs 3–8). Even at a lower running speed of 11 m s ­1 (refs 3, 4, 8), an adult Tyrannosaurus would have been near or above its maximum muscular capacity. A walking tyrannosaur could have adopted more extended limb joints to lower the GRF moment arms (R) and used double limb support to reduce the GRF, decreasing the T required for walking within reasonable bounds ( Table 2 : models Trex_4 and Trex_lowest). However, our calculations suggest that even a walking tyrannosaur required activation of a large fraction of its extensor muscle volume, at considerable metabolic expense.

These conclusions should apply to all larger dinosaurs, invalidating arguments that tyrannosaurs were too slow to prey on large contemporaries 3 such as Triceratops . Tyrannosaurus shows the most extreme cursorial (that is, locomotion­related) specializations of larger theropods 5 – 9, but even it was probably a slow runner, at best. Therefore we infer that the numerous lineages of theropod dinosaurs that evolved enormous sizes 9 independently reduced their running ability. Conversely, reduction of body size and relative increases of extensor muscle sizes and moment arms probably increased running ability in maniraptoran theropods, especially birds 15, 16. Methods

The minimum mass of muscle (mi) required to produce the joint moment M musc to maintain static equilibrium about any joint i is a function of the muscle density (d), multiplied by the volume (V), divided by the fraction of active muscle volume (c). V is equal to the muscle fibre length (L), times the cross­sectional area (A), divided by the cosine of the pennation angle of the muscle fibres (cosv) 12–14. Furthermore, A is equal to the muscle force (F) divided by the stress (j). Finally, F must be the M musc required to stabilize each joint,divided by the mean extensor muscle moment arm (r) 12–14. Combining these expressions to solve for the extensor muscle mass required to act about a particular joint i (mi; expressed as a percentage of body mass, m body) produces:

m i 100 M musc Ld = j crm body cosv 1

These parameters do not depend greatly on the physiology of the animal 22, so the equation holds for both warm­ and cold­blooded animals.

Estimating the joint moment Mmusc

In order to estimate M musc (and hence mi), we used MATLAB (The Mathworks) software to compute the joint moments needed to maintain static equilibrium in a particular limb orientation. To maintain equilibrium, muscles must exert net muscle moments about joints that balance equal and opposite moments incurred by external and internal forces, such as the ground reaction force (GRF) and segment weights (W b, W t, W s and W m in Fig.1 ). These moments can be calculated in two dimensions by drawing a set of free­body diagrams and applying the three equilibrium equations (S F x 0, S F y 0, S M 0).

This procedure is appropriate for standing, and we explain below how it can be applied to running. We summed mi for all four limb joints to estimate T, the total extensor muscle mass required per leg, as a percentage of m body.

Choosing G

We multiplied the GRF magnitude in the free­body diagram analysis by a factor G, the ratio of the GRF to body weight (m body g, with g 9: 81 m s 22), to estimate the M musc needed to support the body on one leg at mid­stance of fast running. At mid­stance of running, the body centre of mass is at its lowest point accelerating upwards, but inertial moments are miniscule relative to the moments of the GRF,so mid­stance is approximated as quasi­static 12–14,23. The value of G was set at 2.5, which is a reasonable value for fast running or hopping bipeds 12–14,24,25.

Determining forward velocity

To determine an approximate forward velocity that would be consistent with G 2:5 for Tyrannosaurus , we can use the notion of dynamic similarity, such as the Froude number (Fr), the ratio of centripetal to gravitational forces 26, calculated as Fr

velocity 2 = hip height 3 g. Our value of G 2:5 for Tyrannosaurus high­speed running is comparable to the value (G 2:7) estimated for an ostrich 27 running at 12 m s ­1 with Fr 16. For Tyrannosaurus (hip height is roughly 2.5 m), Fr 16 implies an average forward speed of almost 20m s ­1. Therefore our model assumes a GRF magnitude consistent with the faster estimates of Tyrannosaurus running speed 5–7. In theory, at

Fr. 1, an animal should switch from a walk to a run 26. Consequently the maximum walking speed that an adult tyrannosaur might have used was roughly 5 m s ­1 (11 m. p.h.), which is still faster than speed estimates from known tracks of large theropods 9.

Model parameters

To reconstruct running mechanics in extinct dinosaurs, we modelled a small adult theropod (Coelophysis), a small juvenile tyrannosaur, and an adult Tyrannosaurus (Supplementary Information) . Functional segment lengths (distances between centres of joint rotation), masses,and centres of mass were measured from dissections for the extant taxa, or approximated for the extinct taxa.Hip, knee, ankle and toe joints connected these segments and were given joint angles.These parameters (see Supplementary Information) were used in a free­body diagram analysis ( Fig. 1 ) to calculate M musc for equation (1).

We entered other parameter values ( Table 1 ) into equation (1) to estimate T. The values of L, v and r were measured from dissections for the extant taxa, or approximated for the extinct taxa. The muscle density (d) was set at 1:06 3 10 3 kg m23 as in typical skeletal muscle 28, and the muscle stress (j) was entered as 3:00 3 10 5 N m22, the maximum isometric stress frequently measured 22. Because we were estimating the minimum mass of muscle required to produce M musc, we set the fraction of active muscle volume (c) at 1. Muscle moment arms (r) were estimated for extinct taxa by applying muscle reconstructions 15, 16 to skeletal material, at appropriate joint angles.

T constraints

The ratio of actual extensor muscle mass to T, the required mass (both terms as a percentage of m body) must be at least 1 for a bipedal animal to be able to run quickly; otherwise the actual muscles would be unable to generate the required forces. For extinct animals, we cannot measure the actual muscle masses, but as the estimated T increases, good running performance becomes increasingly unlikely.If T is more than 50% m body per leg (100% m body total), running at Fr 16 is certainly impossible.

Figures

Figure 1 Explanation of free­body diagram analysis of body segments.Skeletal illustration modified from ref. 6. The initial Tyrannosaurus model (Trex_1) is shown in right lateral view and (x, y)­coordinate space,with the origin located at the toe joint. Pelvic pitch,hip, knee, ankle and toe joint angle definitions are shown (see Supplementary Information). One of the angles is redundant (four angles suffice). The ground reaction force (GRF) is vertical (typical for mid­stance12–14) and acts at a distance R from the toe joints.The body segment weights (Wb, Wt, Ws and Wm for the trunk,thigh,shank and metatarsus) are also shown.A free­body diagram was used to calculate the internal moments about each joint. For example, about the knee joint (see inset), the moment that knee extensor muscles must generate (Mk) is equal to the ankle contact force (­Fa) times its respective moment arm, plus the gravitational moment of the shank segment and the ankle moment (­Ma).

Figure 2 Limb orientation used for model Trex_1. The values of mi, the percentage of body mass as extensor muscle acting about each joint (muscle moment action shown as a red arrow) required to maintain static equilibrium at mid­stance during fast running are shown in red. Actual hindlimb bones were digitized from Tyrannosaurus specimen MOR 555 (Museum of the Rockies; Boseman, Montana).

Figure 3 Estimated extensor muscle mass (T, as a percentage of body mass per leg) required to run quickly. Data are from various models and extant species plotted against log(mbody) to illustrate the scaling of T. Larger runners need a larger fraction of their body allocated to extensor muscle mass.Three shades of grey indicate the likelihood of running ability, based on estimated T. Very low estimated T implies a good chance of being a capable runner. Very high estimated T signals little chance of being a capable runner. Intermediate values of estimated T are inconclusive, and running ability in this case depends on the ratio of actual extensor muscle mass to T. Values of T greater than 50% per leg,or greater than 100% in total,are impossible.The solid line represents the case of scaling a chicken isometrically up to 6,000 kg.

Tables

Table 1 Muscle anatomical data entered in equation (1) to estimate T

Hip Knee Ankle Toe .............................................................................................................................................................................
Alligator
Mmusc (N m) 16	12	12	4.7
L (m) 0.092	–	0.037	0.0020
v (8) 18	–	21	19
r (m) 0.019	–	0.017	0.0050
mi (% mbody) 4.9	0	1.7	1.1
T (% mbody)			7.7
Gallus
Mmusc (N m) 4.0	­0.30	4.7	2.2
L (m) 0.085	0.051	0.026	0.026
v (8) 0	25	23	22
r (m) 0.038	0.026	0.010	0.0050
mi (% mbody) 0.08	2.0	2.0
T (% mbody)			4.7
Coelophysis
Mmusc (N m) 45	­14	56	44
L (m) 0.17	0.097	0.065	0.037
v (8) 9.0	21	22	21
r (m) 0.080	0.028	0.014	0.0060
mi (% mbody) 1.4	0.73	4.0	4.1
T (% mbody)			10
Small tyrannosaur
Mmusc (N m) 570	­180	580	390
L (m) 0.40	0.19	0.18	0.062
v (8) 9.0	21	22	21
r (m) 0.14	0.057	0.025	0.020
mi (% mbody) 4.2	1.6	11.4	3.3
T (% mbody)			21
Tyrannosaurus ( Trex _1 best guess)
Mmusc (N m) 75,000	­24,000	66,000	49,000
L (m) 1.2	0.52	0.39	0.19
v (8) 9.0	21	22	21
r (m) 0.37	0.22	0.11	0.065
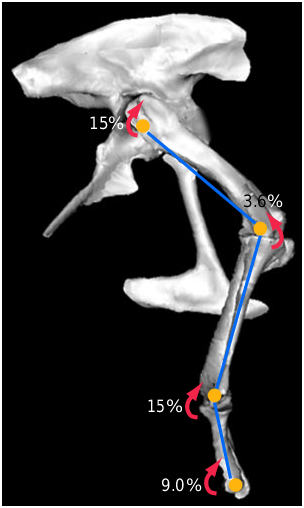
mi (% mbody) 15	3.6	15	9.0
T (% mbody) 43 .............................................................................................................................................................................

Values given are for all four limb joints (hip,knee,ankle,toe). Mmusc is the muscle moment required to maintain static equilibrium during single limb support at mid­stance of fast running (with G 2:5); L is mean muscle fibre length; v is mean extensor muscle fibre pennation angle; r is mean extensor muscle moment arm (means were weighted by physiological cross­sectional area as in refs 12–14); mi is the percentage of mbody needed as extensor muscles about one joint; T is the total percentage of mbody per leg needed as extensor muscle (sum of all four mi values).

Figure 2 Limb orientation used for model Trex _1. The values of mi, the percentage of body mass as extensor muscle acting about each joint (muscle moment action shown as a red arrow) required to maintain static equilibrium at mid­stance during fast running are shown in red. Actual hindlimb bones were digitized from Tyrannosaurus specimen MOR 555 (Museum of the Rockies; Boseman, Montana).

The Mmusc shown is an extensor moment if it is positive, flexor if negative; except at the knee where the converse is true. In the Alligator model, the knee joint mi was set at 0 because the knee Mmusc was a flexor moment and we conservatively assumed that two­joint hip extensors and knee flexors (for example M. caudofemoralis longus) could stabilize both joints. See Supplementary Information for more details.

Table 2 Parameter sensitivity in Tyrannosaurus models

Hip Knee Ankle Toe .............................................................................................................................................................................
Trex_2
Mmusc (N m)	53,000	­56,000	72,000	45,000
L (m)	1.2	0.52	0.39	0.19
v (8)	9.0	21	22	21
r (m)	0.37	0.22	0.11	0.065
mi (% mbody)	10	8.3	16	8.3
T (% mbody)				43
Trex_3
Mmusc (N m)	75,000	49,000	80,000	29,000
L (m)	1.2	–	0.39	0.19
v (8)	9.0	–	22	21
r (m)	0.37	–	0.11	0.065
mi (% mbody)	15	0	18	5.3
T (% mbody)				38
Trex_4
Mmusc (N m)	75,000	6,500	4,400	4,100
L (m)	1.2	–	0.39	0.19
v (8)	9.0	–	22	21
r (m)	0.37	–	0.11	0.065
mi (% mbody)	15	0	0.99	0.75
T (% mbody)				17
Trex_Lgator
Mmusc (N m)	75,000	­24,000	66,000	49,000
L (m)	0.93	0.39	0.37	0.19
v (8)	18	16	21	19
r (m)	0.37	0.22	0.11	0.065
mi (% mbody)	12	2.6	14	9.0
T (% mbody)				38
Trex_Lchick
Mmusc (N m)	75,000	­24,000	66,000	49,000
L (m)	1.1	0.65	0.41	0.33
v (8)	0	25	23	22
r (m)	0.37	0.22	0.11	0.065
mi (% mbody)	13	4.6	16	16
T (% mbody)				50
Trex_lowest
Mmusc (N m)	75,000	6,500	4,400	4,100
L (m)	0.93	–	0.37	0.19
v (8)	0	–	0	0
r (m)	0.37	–	0.11	0.065
mi (% mbody)	11	0	0.87	0.71
T (% mbody) 13 .............................................................................................................................................................................

This shows the effect on the estimate of T (relative to model Trex_1) when we changed limb orientation (models Trex_2­4) or muscle­fibre lengths (model Trex_Lgator and Trex_Lchick, isometrically scaling up L from Alligator (5.91 kg) and Gallus (2.89 kg) to Tyrannosaurus (6,000 kg). As with Alligator ( Table 1 ), models Trex_3, Trex_4, and Trex_lowest had a flexor Mmusc about the knee joint, so the knee mi was conservatively set at 0. Model Trex_lowest shows a combination of parameter values (L from model Trex_Lgator, limb orientation from model Trex_4, and v set at 08) that brought T to its lowest estimated value (see Supplementary Information).