Tyrannosaurus rex
|
publication ID |
https://doi.org/10.1080/02724634.1995.10011257 |
|
DOI |
https://doi.org/10.5281/zenodo.4912560 |
|
persistent identifier |
https://treatment.plazi.org/id/F362885A-FFFB-FFD0-FE08-B387B14C48B8 |
|
treatment provided by |
Jeremy |
|
scientific name |
Tyrannosaurus rex |
| status |
|
INTRODUCTION
Large carnivorous dinosaurs like Tyrannosaurus were the biggest land-living predators in earth history (Far- low, 1993). Because body mass influences, or is at least correlated with, many features of the biology of ani mals ( McMahon and Bonner, 1983; Peters, 1983; Cal der, 1984; Paul, 1988; Alexander, 1989; Dunham et al., 1989; Damuth and MacFadden, 1990; Spotila et al., 1991; Damuth, 1993), estimates ofthe body masses of the largest terrestrial predators are of some theo retical interest. One controversial aspect (of many!) of the biology of large theropods is the top speeds attained by these reptiles. Interpretations of the sprint speed of Tyrannosaurus range from as much as 18-20 meters/second (m/s) ( Bakker, 1986; Paul, 1988) to as little as 7 m/s (Thulbom, 1982). In the present paper we report an estimate of the live mass of Tyrannosaurus rex based on a model res toration of a fairly complete skeleton (Museum of the Rockies [ MOR] 555 ), along with an estimate of an “indicator of athletic ability” (Alexander, 1989:55), or more simply the “strength indicator,” of the femur of this specimen. We then consider the implications of our results for interpretations of the cursorial potential of this very large theropod. Finally, we discuss other matters relevant to interpreting the sprint speed of Tyrannosaurus' , among these, particular attention is given to simple models that consider the risk of injury that this huge predator would face were it to fall while running.
METHODS
An account of the discovery and collection of MOR 555 was presented by Homer and Lessem (1993). This specimen is a representative of what is said to be the gracile morph of Tyrannosaurus rex (Horner and Les sem, 1993; cf. Carpenter, 1990; Molnar, 1991; Larson and Frey, 1992). One of us ( M.B.S.) sculpted a model ( 1/20 scale) life restoration of the dinosaur, based on MOR 555 ( Fig. 1 View FIGURE 1 ); selected estimates of dimensions of the “prototype”, based on Smith’s model, are sum marized in Table 1 View TABLE 1 . We determined the volume of this model by measuring the difference in the model’s weight in air and when submerged (cf. Alexander, 1985, 1989). Cavities in the model interior were filled with Duco cement, which was allowed to harden before measurements were made. Volume determinations were done at room temperature; measured water temperatures during the runs ranged from 18-21 °C. Three such model volume determinations were made. We checked the accuracy of our experimental tech nique by estimating the model’s volume in another way: by collecting water displaced from a container when the model was completely submerged. The mo del’s volume was estimated either by weighing the displaced water, or measuring its volume directly. Model volumes estimated by this water overflow method were a little higher, and much less precise (in the statistical sense), than those measured by determining the difference of the model’s weight in air and in water; this presumably reflects greater experimental error in measuring model mass by water overflow than by the method used by Alexander. We then calculated the volume of the full-sized, pro totype dinosaur by multiplying the model’s volume by the cube of the inverse of the scale of the model (i.e., by 203 = 8,000). Estimating the live mass of the pro totype from its volume depends on the specific gravity (SPGR) of the living dinosaur. This was probably comparable to that of water (Alexander, 1989), or a little less ( Paul, 1988), depending on (among other things) the degree of pneumaticity of the animal’s bones. We made two estimates of the live mass of MOR 555 , one (SPGR assumption 1) reflecting the assumption that the creature’s specific gravity was 1.00 (Alexander, 1989), and the second (SPGR assumption 2) that the dinosaur’s specific gravity was 0.85 ( Paul, 1988).
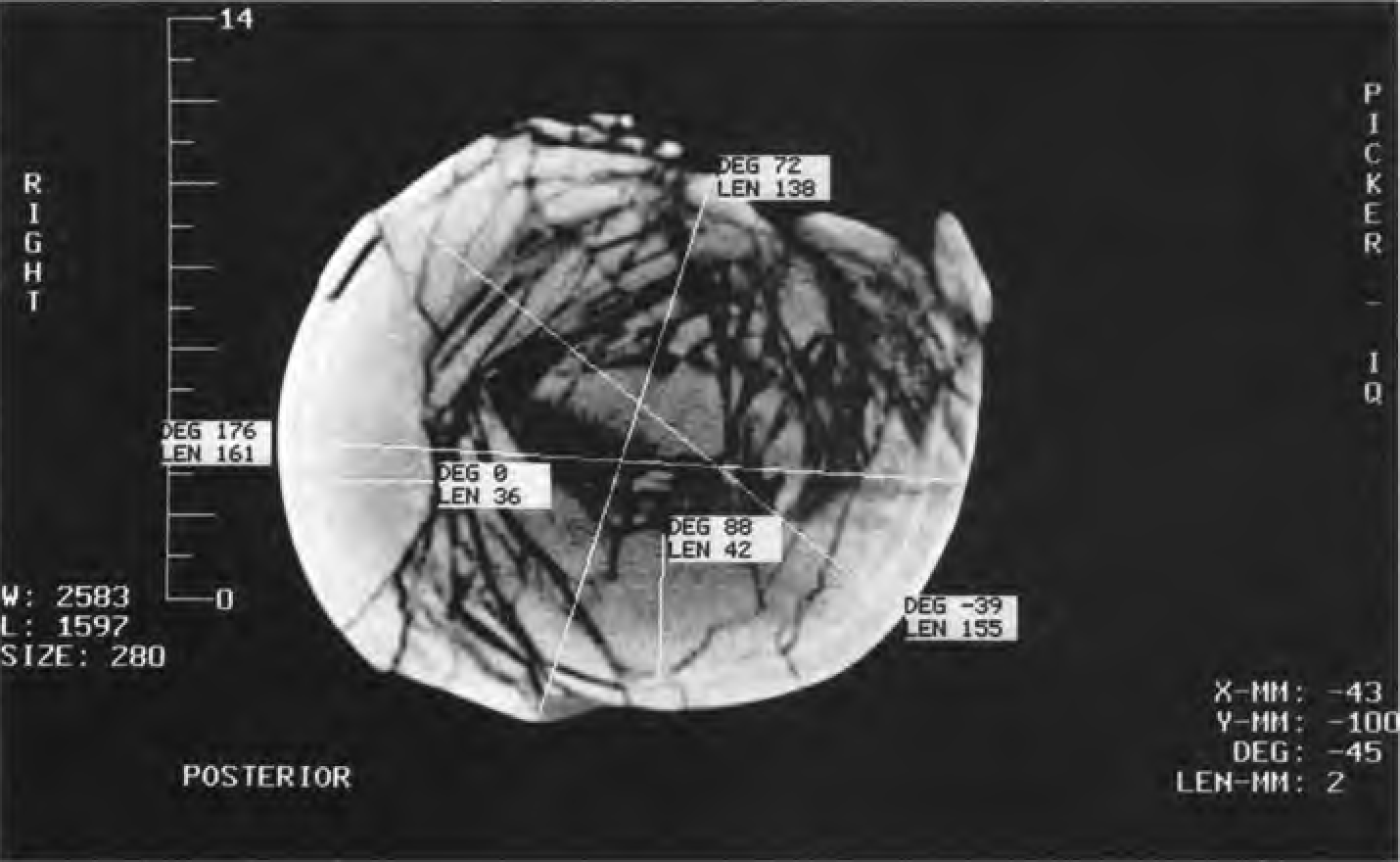
The mass estimate was then used to estimate Alexander’s (1989) strength indicator, a quantity that describes a long bone’s capacity for resisting bending stresses associated with vigorous activity. We measured the length, midshaft anteroposterior and mediolateral diameters, and midshaft circumference of the right femur of MOR 555 ( Table 2 View TABLE 2 ). Unfortunately, a CT-scan of the midshaft of this bone ( Fig. 2 View FIGURE 2 ) indicated that it had been slightly crushed. Our estimate of the section modulus of this bone, and our estimate of the strength indicator of Tyrannosaurus , could be made only by using certain assumptions.
We assumed that the before-crushing cross-sectional shape of the femoral midshaft was nearly circular (cf. Osborn, 1906:fig. 10 View Fig. 10 ), and estimated its external diameter as the average of the anteroposterior and mediolateral diameters of the bone as now preserved ( Table 2 View TABLE 2 ; average =153 mm). We made several measurements of the femur’s cortical thickness from the CT-scan, and used the average of these (36 mm) for further calculations. We assumed that the pre-crushing marrow cavity was circular in shape, and estimated the diameter of the marrow cavity by subtracting twice the value of the average cortical thickness from our estimate of the external midshaft diameter.
Because we assumed circular cross-sectional shapes for the entire femoral midshaft and for the marrow cavity of MOR 555 , we calculated the section modulus for each of these as 0.78 x radius3 (Alexander, 1989). The section modulus of the marrow cavity was then subtracted from that of a solid bone (no marrow cavity) of external dimensions comparable to the femoral midshaft of MOR 555 (see Farlow, 1990:table 1) to obtain an overall section modulus estimate for the femoral midshaft.
Like Alexander (1985, 1989) we assumed that the bending force acting on the femur acts halfway along the length of the femur. We therefore calculated the strength indicator for MOR 555 as
Total length of the animal, snout to tailtip, measured along the curve of the dinosaur’s back—1,196 cm
Head length— 162 cm
Neck length —120 cm
Body length from in front of the shoulder to the back of the hip—320 cm
Tail length—594 cm
Height of the top of the head above the ground—460 cm
Height of the lower edge of the lower jaw above the ground—346 cm
Height of the top of the hip above the ground—356 cm
Height of the lowest spot on the belly (at distal end of pubis) above the ground—146 cm
Maximum dorso-ventral body depth—208 cm
Maximum width across hips—96 cm
Maximum chest width—98 cm
(section modulus of femur midshaft)
÷ [(animal mass)(1/2 femur length)
x (gravitational constant)]
and multiplied the result by 109 newtons/giganewton to express the strength indicator in units of m2/giganewton.
RESULTS
As restored by Smith, Tyrannosaurus rex is very slimly built for its size. The dinosaur is quite deepbodied, and its torso extraordinarily narrow in mediolateral dimensions ( Table 1 View TABLE 1 ; Fig. 1 View FIGURE 1 ). Although reminiscent of Paul’s (1988:341) skeletal restoration of T. rex (based on American Museum of Natural History 5027 and Carnegie Museum of Natural History 9380), Smith’s restoration has a transversely narrower body trunk, and a relatively longer tail whose proximal end is narrower from top to bottom.
Three body mass experimental determinations yielded estimates ranging 6,319-6,329 kg, with an average of 6,325 kg (SPGR assumption 1), or 5,371 5,380 kg, with an average of 5,376 kg (SPGR assumption 2).
The section modulus obtained for the femur of MOR 555 is 0.00030 m3.4For * * *an * estimated body mass of 6,300 kg, the strength indicator for Tyrannosaurus rex is 7.5 m2/giganewton; for an estimated mass of 5,400 kg, the strength indicator is about 9 m2/giganewton. The assumption of circular shapes for the non-crushed femur midshaft exterior and marrow cavity does not greatly affect the values of the strength indicator. If we assume that the measured values ofthe anteroposterior and mediolateral midshaft diameters given in Table 2 View TABLE 2 are close to the real values, and that (as suggested by some of our CT-scan images) the marrow cavity was elliptical in shape (with an anteroposterior diameter of about 46 mm and a mediolateral diameter of about 92 mm), then the strength indicator for a 6,300-kg Tyrannosaurus is about 8 m2/giganewton (using the formula for the section modulus of an elliptical section from Alexander, 1983:table 1).
DISCUSSION
Body Mass of Tyrannosaurus rex
Our estimate of the live mass of MOR 555 is roughly in the middle of previously published body mass estimates of Tyrannosaurus rex ( Table 3 View TABLE 3 ). Some of the previously published estimates (e.g., Colbert, 1962; Alexander, 1985; Paul, 1988), like ours, have been based on measurements of the volumes of scale models. The accuracy of such determinations obviously depends on the quality of the model restoration.
Potentially the greatest source of error in our estimate of the live mass of MOR 555 stems from inaccuracies in modeling the live animal (e.g., in reconstructing its musculature) that might result in departures from the 1/ 20 scale assumed for the linear dimensions of the model. These will be greatly magnified when the reciprocal of the scale is cubed to determine the volume of the prototype; only a little error in the model results in a great error in the volume of the fullsized animal. For example, if the overall scale of the model is actually closer to V18 than V20, the body mass estimate of the prototype drops to about 4,600 kg (SPGR assumption 1) or 3,900 kg (SPGR assumption 2). There is obviously no way of checking the extent to which this kind of error exists in our mass estimate for the living dinosaur, and we will assume that the scale of our model of the live animal really is to
Other estimates ( Anderson et al., 1985; Campbell and Marcus, 1992) of the mass of Tyrannosaurus have been based on regressions of body mass on femoral midshaft circumferences of living mammals or birds. It is noteworthy that previously published body mass estimates for T. rex based on regression analyses tend to be lighter than those based on model volume determinations. The same result is obtained for MOR 555 . If the mass of this dinosaur is estimated from the midshaft circumference of its femur ( Table 2 View TABLE 2 —but recall that the femur is crushed, casting some doubt on our measurement of its circumference), the value obtained from the equation of Anderson et al. (1985) is 4,030 kg, and that obtained from the equation of Campbell and Marcus (1992) is 3,000 kg.
Although we are uncertain why the equation of An- derson et al. (1985) yields a smaller mass estimate than the one obtained from our model (unless this reflects the small number of [perhaps questionable] data on which the regression equation is based), a plausible reason for the even lighter mass estimate obtained by Campbell and Marcus is readily apparent. The latter authors used a regression of live mass against femoral circumference in birds to estimate the mass of Tyrannosaurus . However, the ratio of femoral cross-section diameter to femoral length is much greater in birds than in non-avian theropods (Gatesy, 1991), presumably due to differences in the dynamics of locomotion in typical theropods as opposed to birds ( Gatesy, 1990, 1991). For a given body mass, a bird probably has a much shorter and stouter femur than did a non-avian theropod, and this in turn may mean that using the avian relationship between femoral circumference and body mass will considerably underestimate the live mass of a non-avian theropod.
On the assumption that our mass estimate of about 6,000 kg for MOR 555 is reasonably accurate, it is worth noting again that this specimen is a representative of what is said to be the gracile morph of Tyrannosaurus rex ( Homer and Lessem, 1993). We would not be surprised if the robust morph were considerably heavier, with a body mass of 7,000 or even 8,000 kg. Furthermore, as noted by Paul (1988), the presently known specimens of Tyrannosaurus might well be average-sized adults, and not the very biggest individuals.
Strength Indicator of Tyrannosaurus rex
Alexander (1985, 1989) estimated the strength indicator of Tyrannosaurus to be about 9.0 m2/giganewton. Given that the model he used in his mass determination was not particularly good (Paul, 1990), that our mass estimate is based on a more complete specimen than any known at the time the model used by Alexander was constructed, and that Alexander’s model might not have been based entirely on the same specimen for which he obtained data on the femoral section modulus, we think that our data for estimating the strength indicator of Tyrannosaurus rex are better than Alexander’s. Even so, our estimate of the strength indicator of the animal (7.5-9.0 m2/giganewton) is remarkably close to Alexander’s.
Alexander (1985, 1989) and Alexander and Pond (1992) calculated the strength indicator for a number of living animals, and found good agreement between values calculated from the femur and the known cursorial performance of those animals. Our estimate of the strength indicator of Tyrannosaurus rex is a little higher (as noted by Alexander) than that of an African elephant (7.0 m2/giganewton) and, again as noted by Alexander, much less than that of a human being (15 m2/giganewton), let alone runners like the ostrich (44 m2/giganewton—although differences in the way the ostrich carries its femur from the way T. rex presumably did may cause the ostrich’s very high strength indicator value to be inappropriate for comparison with that of a non-avian theropod), the white rhinoceros (see below), and the African buffalo (22 m2/giganewton). Although Farlow (1990) suspected that Alexander’s strength indicator might underestimate the cursorial potential of theropods, it seems unlikely, given our results, that the strength indicator underestimates the running ability of Tyrannosaurus to the point that this dinosaur could have attained speeds comparable to those ofthe fastest modem cursorial birds and mammals.
A note of caution must be stated, however. As noted by Farlow (1990), the value of the strength indicator is greatly influenced by the body mass estimate. We believe our estimate of the live mass of MOR 555 to be the best presently available for T. rex , but it could nevertheless be inaccurate, as already discussed. This would in turn affect the accuracy of our estimate of the strength indicator. For example, if the true live mass of MOR 555 were about 4,000 kg, as suggested by the equation of Anderson et al. (1985), the strength indicator for the dinosaur becomes 12 m2/giganewton. Although much higher than the value obtained when using a mass estimate from Smith’s model, the magnitude of the increase is not enough greatly to affect our interpretation of the running ability of Tyrannosaurus .
Even if our estimate of the strength indicator of MOR 555 is accurate, however, this nonetheless represents the value for a single individual of Tyrannosaurus rex , and it may be risky to generalize about the cursorial potential of the species on the basis of what amounts to a single data point (or two, given that Alexander’s estimate of the index was based on another individual of the species). Furthermore, our interpretations about the cursorial potential of Tyrannosaurus apply only to adult animals. It is not inconceivable that younger, smaller individuals of the species were not subject to the same constraints of locomotor performance that we think affected adults.
The biggest living galloping mammal is the white rhinoceros { Ceratotherium simum ), an animal that attains a body mass about half that of our estimate for MOR 555. Alexander and Pond (1992) reported that this species runs at speeds of as much as 7.5 m/s; Nowak (1991) reported that the white rhinoceros can run at 40 km/hr (11 m/s) for short distances (a speed estimate that Alexander [pers. comm.] believes should be taken with considerable caution). This suggests that it is not, in principle, impossible for a large, heavy animal to be a runner. However, Alexander and Pond (1992) calculated the strength indicator for the femur of an immature female C. simum to be 26 m2/giganewton, much greater than our estimate for T. rex .
Additional Constraints on the Cursorial Potential of Tyrannosaurus rex
Body Size, Posture, and Maximum Running Speed— With increasing body mass, both mammals and birds adopt increasingly more erect, less flexed stances (Mc Mahon and Bonner, 1983; Biewener, 1989a, b, 1990; Bertram and Biewener, 1990; Gatesy and Biewener, 1991) in order to maintain uniform skeletal stresses. This results in a lower limb excursion angle for large as opposed to small-bodied species. At body masses greater than about 200 kg, however, it is no longer possible to maintain uniform skeletal stresses through postural adjustments alone, necessitating more robust bone elements and a probable decline in sprint speed ( Garland, 1983; Garland etal., 1988; Biewener, 1989a, b, 1990; Chappell, 1989; Bertram and Biewener, 1990). This suggests that a 6,000 kg animal like Tyrannosaurus is unlikely to have been as fast or maneuverable a runner as the best living cursors (or smaller-bodied theropods, either, for that matter).
This interpretation is reinforced by consideration of the construction of the dinosaurian hip joint. Hotton (1980) noted that the femoral component of the hip joint of dinosaurs is cylindrical, rather than spherical, as it is in mammals. Hotton suggested that this made dinosaurs less able than mammals to make adjustments for irregularities of footfall during running. If true, this constraint should apply particularly to very large forms like Tyrannosaurus , and less to smaller theropods like ornithomimosaurs ( Hotton, 1980). The cursorial performance of huge theropods might have been restricted to prevent sudden, accidental loadings beyond the capacity of the hip joint to handle (cf. Biewener, 1989a, b, 1990; Bertram and Biewener, 1990).
Coombs (1978) noted that fast-running animals tend to have relatively longer lower than upper limb bones. Using an analytical technique that corrects for phylogenetic relationships, Garland and Janis (1993) showed that limb proportions have some utility in predicting sprint speeds in mammals, but that so many other factors affect limb length ratios as to prevent any simple estimate of speed from limb proportions.
Tyrannosaurids tend to have lower tibia/femur and metatarsus/femur length ratios than do smaller-bodied theropods of unquestioned cursorial ability (omithomimosaurs) to which they may be related ( Coombs, 1978; Gatesy, 1991; Holtz, 1994), although these ratios are in some cases higher in tyrannosaurids than in smallerbodied taxa of other, more primitive, clades of theropods ( Holtz, 1994). This is at least consistent with our interpretation that Tyrannosaurus may have been less fleet than many smaller theropods, particularly omithomimosaurs.
The Risk of a Fall— There is also the matter of what McMahon and Bonner (1983: 139) described as “one of [the] most dangerous pieces of bad luck” for a dinosaur as large as Tyrannosaurus— an accidental fall (cf. Homer and Lessem, 1993). It seems reasonable to suppose that the more quickly the dinosaur moved, the greater the chance of a mistake in the way a foot hit the ground, and thus the greater the risk of a fall. We think it likely that, whatever the biomechanical limits of the skeleton of Tyrannosaurus , the dinosaur may have been loath to attempt sprints during which the risk of falling would have been great.
A quadruped is perhaps less likely to trip and fall during rapid locomotion than a biped is. Should it lose its balance while moving forward, there is a chance that one set oflimbs can correct for a mistake in footfall made by the other set. Furthermore, because there are two forelimbs and two hindlimbs, the quadruped may be more stable—and better able to correct for errors of foot placement—than a biped in the transverse direction as well.
Judging from a photograph of a white rhinoceros in Nowak (1991), the height of the animal’s belly above the ground should be about half a meter. In contrast, we estimate that the belly of MOR 555 was about three times that distance above the ground ( Table 1 View TABLE 1 ). The lower edge of the head of a galloping rhinoceros is carried at about the same height as the ventral edge of the belly (Alexander and Pond, 1992:fig. 1). In contrast, Tyrannosaurus , a biped, carried the lower edge of its head about 3.5 meters off the ground ( Table 1 View TABLE 1 ).
Given that white rhinoceroses do gallop, they clearly are prepared to risk injury should they fall. This risk of injury is probably mitigated by the short distance over which a fall would take place. Furthermore, the body of a rhinoceros is rather broad from side to side, and so the force of impact against the ground, were the animal to drop straight down and hit its belly during a fall, would be distributed over a fairly large surface area.
Consider, in contrast, the fate of a tripping Tyrannosaurus ( Fig. 3 View FIGURE 3 ). It is roughly twice as heavy as a white rhinoceros. If the hindfoot opposite the one that stumbles cannot be brought forward quickly enough to stop the fall, the tyrannosaur has a problem: it lacks forelimbs long enough, or strong enough, to catch itself before its body and head hit the ground. It has a longer distance to fall than a rhinoceros does, and, if it lands on its belly, rather than its side (thus minimizing the vertical distance of the fall), the force of impact will initially be concentrated on a relatively smaller surface area (in comparison with its body trunk mass, ignoring the tail) than is true for the rhinoceros. Furthermore, the dinosaur’s head has a very long way to fall. We think that the risk of serious, or even fatal, injury would be much greater for the dinosaur than the rhinoceros, a belief that we attempt to quantify later.
Injury or death during a fall results from “tissue damage... caused by the absorption by the body of the kinetic energy accumulated during the period of free fall” ( Buckman and Buckman, 1991:331). The magnitude of damage depends on the distance over which the animal falls, the animal’s mass, the body’s orientation as it hits the ground, and how rigid or yielding is the substrate on which the animal lands ( Buckman and Buckman, 1991; Mathis et al., 1993).
Although determining the exact magnitude of forces involved in the fall of a Tyrannosaurus is virtually impossible, we can present some simple models that at least illustrate the relevant parameters. If a running animal trips and falls, the force it experiences on impact with the ground has both vertical and horizontal components, which can be treated independently. The vertical component is unaffected by the animal’s running speed, but the horizontal component is a direct consequence of the creature’s speed.
The Vertical Component of Impact Force—Our model of the vertical force affecting a falling animal is illustrated in Figure 4 View FIGURE 4 . This model can be applied to the force of impact against the ground of either the animal’s torso or its head. To apply the model to T. rex , we assume that the dinosaur’s torso (here considered the body without the head, tail, and those “free” portions ofthe hindlimbs that extend below the ventral edge of the body trunk) has a mass of about 4,524 kg (estimated by subtracting the estimated volumes of our model’s head, “free” hindlimb portions, and tail [determined by water displacement] from the model’s total volume; we assume a total body mass of 6,000 kg), and its head a mass of 695 kg.
Prior to falling ( Fig. 4A View FIGURE 4 ), the center of mass C of the animal’s torso or head is some distance y above the lower edge of its torso or head, which is in turn some distance h1 above the ground. After the fall ( Fig. 4B View FIGURE 4 ), the animal makes a hole in the ground that is some depth h2. As the torso or head hits the ground, it deforms or squashes by some amount that changes the distance from the center of mass to the ventral edge of the torso or head from y to y1; we call this change the “squash distance” δy (=y — y1). The change in the potential energy ofthe torso or head as a result offalling is given by
W(h1 + h2 + δy),
where W is the weight of the torso or head. By the Work-Energy Theorem and Newton’s Third Law ( Cutnell and Johnson, 1992), this quantity must equal the work, Fv (h2 + δy), done by the average net vertical impact force Fv. Consequently
Fv = W(h1 + h2 + δy) Fv h 2 + δy
Moreover, because Fv = mass x av, where av is the vertical impact deceleration, and because W = mass x g (where g is the gravitational constant), we find
av = (h1 + h 2 + δy) gh2 + δy
Values of the various parameters in our model are estimated from Table 1 View TABLE 1 , or are what seem to us reasonable guesses. For the dinosaur’s torso, we assume that h1 is 1.46 m. The weight of the torso is its mass multiplied by the gravitational constant g (9.81 m/s2).
Our estimate of the impact force is obviously greatly affected by the height of the dinosaur’s torso above the ground and the torso’s weight. The estimate is less obviously, but perhaps even more critically, affected by the assumed values of the depth of the hole made by the torso as it hits the ground, and by how much the torso deforms upon impact. These last two parameters may be inversely related, depending on the firmness of the substrate. If our Tyrannosaurus were unlucky enough to fall on solid rock, the depth of the hole created would likely be nil, but the animal’s squash distance would probably be very large. This is unlikely to be favorable for the animal; a large squash distance would surely be associated with considerable damage to the dinosaur’s internal organs.
On the other hand, if a falling Tyrannosaurus were to land on a soft, muddy substrate, the force of impact would be less, because h2 could be quite large. The dinosaur might well survive a fall under those conditions. Similarly, if it fell in an area where the ground was thickly carpeted with lush vegetation, the dinosaur’s fall might be slowed enough as it fell through the plants to ensure its survival. In this scenario, the equivalent of h2 would again be large.
Such conditions may have been widespread in the environment of Tyrannosaurus ( Russell, 1989) . However, if the ground was soft enough that a falling tyrannosaur would make a very deep hole when it landed, this would probably not be the kind of situation in which an enormous animal would be able to run quickly; the creature would likely sink too deeply into the substrate with each step. Similarly, it is difficult to imagine a huge animal trying to move at speed through thick vegetation. If Tyrannosaurus was structurally capable of running rapidly, we suspect that it would only have done so on rather firm substrates in relatively open settings (e.g., the mid-Maastrichtian “open fern and palmetto-dominated vegetation” reconstructed by Wing et al., 1993). Consequently high-h2 versions of our model are probably not relevant to the question of whether Tyrannosaurus could have survived a fall while running.
Consequently we assume a rather modest value of h2, 0.2 m. We also assume that δy is 5% of the torso’s vertical depth (vertical depth being estimated by subtracting 1.46 m from 3.56 m; Table 1 View TABLE 1 ), or 0.105 m.
Using our estimates of, or assumptions about, the values of parameters in the preceding equations, the net vertical force Fv acting upon the torso at impact is estimated to be roughly 260,000 newtons (N), producing a deceleration of 6 g. In like manner we estimate that h1 for the head is 3.46 m, h2 is once again 0.2 m, and δy is 0.057 m. The impact force of the head is then estimated as 99,000 N, with a deceleration of 14 g. This could be an underestimate, because we have assumed that the head would make as deep a hole in the ground upon impact as the torso would.
We emphasize that the values of Fv and av are unaffected by the animal’s ground speed at the time of its fall. It could drop while standing still and the values would be the same. However, because the animal is less likely to be able to regain its footing if it falls while running rapidly than if it trips while walking slowly, or loses its balance while standing motionless, our calculations are relevant to describing the fate of the dinosaur if it falls while running. Furthermore, the vertical components of impact force and deceleration interact with the horizontal components in determining the overall forces and decelerations that the falling animal experiences.
The Horizontal Component of the Impact Force, I: A Simple, One-Stage, Fixed Skid Distance Model
We first present a model in which the distance that an animal slides along the ground after a fall is fixed at 3 meters.
The horizontal component of the impact force, Fh, depends on the kinetic energy of the running dinosaur and the distance the falling animal slides after impact, d. Applying the Work-Energy Theorem of physics ( Cutnell and Johnson, 1992),
mass x velocity2 Fhd = 2 and 2
mass x velocity2
Fh = 2d
Furthermore, because Fh = mass x ah,
velocity2 ah — 2d
where ah is the horizontal deceleration. Dividing ah by 9.8 m/sec2 gives the corresponding number of “g’s.” Note that ah is independent of the animal’s mass for a given velocity and “skid distance” d.
If we assume that a 6,000 kg Tyrannosaurus could run at a speed of20 m/s (cf. Bakker, 1986; Paul, 1988), and that it would skid 3 m along the ground after a fall sustained while running at that speed, then the average horizontal impact force on the 4,524-kg torso would be some 300,000 N, or 7 g. The average total net force experienced by the falling dinosaur’s torso would be the resultant of the vectors of horizontal and vertical forces, initially some 400,000 N, or 9 g. Similarly, the 695- kg head would experience in the same fall an Fh of 47,000 N, or 7 g, and a total net force of 110,000 N, or 16 g. Because our estimated values of Fv and av affecting the head may be underestimates, the values of the net force and deceleration affecting the head could be underestimates as well.
The Horizontal Component of Impact Force, II: a More Complex, Two-Stage, Variable Skid Distance Model
Our assumption that a Tyrannosaurus that fell while running at 20 m/s would skid 3 meters seems reasonable, but could be questioned. This uncertainty about the stopping distance leads us to consider a more refined model (available as a computer program from J.M.R.) in which the coefficient of sliding friction gk is assumed to be the same for all animals falling on a given surface.
We model the fall of the running animal as a twostage process. During the first stage of the fall the animal experiences both horizontal and vertical deceleration; in the second stage only horizontal deceleration continues.
The impact speed with which our falling animal initially hits the ground will be the square root of the quantity 2ghi (cf. Cutnell and Johnson, 1992). Once impact begins, the animal’s vertical fall will be arrested during some time tv. During this time the animal will continue to move vertically through the distance h2 + 5y, as the impact punches a hole in the ground and deforms the animal’s shape. Once the animal’s body ceases to move vertically, its vertical speed will obviously be zero. We can therefore calculate the average vertical speed of the animal’s body, from the time it first touches the ground until it no longer moves vertically, as Vi the initial impact speed.
Given that speed = distance/time, we can rearrange the equation to show that time = distance/speed. In the case of our falling animal,
tv= h2 + δy tv 0.5 √ 2 gh 1
The force of sliding (or kinetic) friction along a surface is the product of цk and the normal (or contact) force between the object and the surface across which
it slides. In the case of our falling animal, the normal force will be
m(av + l)g,
where av, as calculated previously, is the vertical deleration as a multiple of g, and m is the animal’s mass (1 is added to av to allow for calculation of the normal force in the case in which an object is not sliding, but rather is motionless on the ground). The horizontal friction force Fhl during the initial stage of the fall will have a large value, and will equal
цkm (av + l)g.
The momentum of an object is the product of its mass and its velocity. The impulse of a force is the product of the force’s average value and the time during which the force acts. The Impulse-Momentum Theorem relates these parameters (in terms of the effects of a force exerted on an object) by stating that the impulse of a force is equal to the change in momentum of the object to which the force is applied ( Cutnell and Johnson, 1992).
During the initial phase of its fall, the change in momentum of the animal’s head or torso will be
mδv,
where δv is the decrease in horizontal velocity of the animal’s head or torso during time tv. The impulse of horizontal friction force Fhl will be the product of its average value and tv. By the Impulse-Momentum Theorem,
Fhltv = цkm (av + l) gtv = mδv
Canceling the mass m, we have
δv = цk (av + l) gtv
Because force = mass x acceleration (or deceleration), the horizontal deceleration associated with Fhl, ahl,
equals
цk (av + l) g
During time tv the horizontal velocity of the animal decreases from v0, its running speed at the time it begins its fall, to some value (v0 — Sv). The distance dj that the animal skids across the ground during time tv is equal to
(v0 - [O.5δv]) tv
The reasoning here is similar to that involved in the calculation of V The distance over which the fallen animal skids is the product of its average skid speed and the time V The average skid speed is (v0 + [v0 — Sv])/2, which reduces to v0 — (δv/2).
After time tv, the animal no longer experiences vertical motion, and the unfortunate creature is now in the second, exclusively skidding, stage of the fall. The horizontal friction force (now called Fh 2) now takes the smaller value цkmg; av is now zero.
The Work-Energy Theorem ( Cutnell and Johnson, 1992) states that the work done on an object by a net force is equal to the change in kinetic energy of the object caused by the net force. Given that the kinetic energy ofa moving object is equal to (mass x velocity2)/ 2, we can apply the Work-Energy Theorem to the second, sliding phase of the fall of our animal as
m(v0 - δv)2 цkmgd 2 = 2
where d2 is the distance that the animal continues to slide during this second phase, and (v0 — δv) is the velocity of the animal at the beginning of the second phase. We can rearrange this equation to find
d2= (v0 - δv)2 2цkg
Using the same reasoning as before, the animal’s body slides this distance in a time
t2 = d2/(0.5[vo - δv])
For completeness, we add that if v0 is small, the animal’s slide may come to a halt in a time t1 = v0/ahl shorter than tv. In this case there is no second stage of the slide, and d1 = 0.5v0t1, and d2 and t2 = 0.
For the head and torso of Tyrannosaurus we assume цk (a dimensionless quantity) = 0.8. The appropriate value of цk depends strongly on the nature of the terrain. Our choice of values for цk is of course rather arbitrary; it corresponds to the upper end of the scale of kinetic friction coefficients for objects sliding on rough surfaces ( Serway, 1990). Because of the depression made in the ground by the animal’s vertical fall, our assumption that цk is a constant throughout the fall is not completely realistic.
We assume a speed at the time of the fall v0 = 20 m/s. The above formulas yield tv = 0.11 second, during which time the torso experiences a horizontal deceleration of 5.4 g and a horizontal force of 240,000 N for a distance of 1.9 m. After that, in the second stage of the fall, the torso comes to a stop in a further 12.4 m during 1.8 seconds, experiencing 0.8 g and 35,500 N of frictional force. The total slide distance of 14.3 m is considerably less than the distance d' = 26 m predicted by the formula
d' = v02/(2цkg),
which formula neglects the fact that the friction force is much greater during the short vertical collision time.
Other scenarios based on our model are summarized in Table 4 View TABLE 4 , and discussed in the next section of our paper.
Would a Tyrannosaurus Survive Its Fall?
On the assumption that our estimates of the forces and decelerations affecting a falling Tyrannosaurus are somewhat realistic, we must ask whether the dinosaur is likely to have survived forces and decelerations of the calculated magnitudes. There are obviously no data that are directly relevant to this question, but we can approach the matter in an indirect fashion: by returning to our comparison of the consequences of a fall for a white rhinoceros and for a Tyrannosaurus .
One-Stage, Fixed Skid Distance Model—The value of h1 is about three times greater for the torso of the dinosaur than the torso of the rhinoceros. The difference in torso weight of the two animals is harder to estimate; even though the dinosaur’s total weight is larger than the mammal’s, a greater fraction of body weight in the dinosaur than the mammal consists of tail and limbs. As a rough estimate, we might suppose that the torso of Tyrannosaurus is 1.5 times heavier than that of Ceratotherium . If so, and if δy and h2 are assumed to be the same in falls of the two animals (probably not a completely realistic assumption), then the vertical deceleration of the torso of Tyrannosaurus would be 3 times that of the torso of the rhinoceros (6 g for the dinosaur, and 2 g for the rhinoceros); the corresponding vertical force would be 4.5 times larger for Tyrannosaurus .
Similarly, if a rhinoceros that had been running at a speed of 7.5 m/s fell and slid 3 meters, its torso would experience a horizontal deceleration of only 1 g, compared with the much larger 7 g obtained for Tyrannosaurus running at 20 m/s.
We did not do a separate calculation for the head of the rhinoceros, because we had no basis for estimating its mass. However, the rhinoceros’ head is smaller than that of Tyrannosaurus , and it is carried much closer to the ground than the dinosaur’s (roughly half a meter as opposed to 3 1/2 meters). As a result, the difference in total net force of impact, and in deceleration, between the dinosaur and the rhinoceros would be much greater for the head than for the torso.
As calculated above, the total deceleration of the impacting head of Tyrannosaurus in our one-stage fall model is 16 g, as opposed to 9 g for the torso. Consequently the impact of the dinosaur’s head might cause the animal more damage than the collision of its torso with the ground.
Even though our calculations are surely unrealistic to some extent, it is apparent that a rapidly running Tyrannosaurus had to be prepared to risk impact forces and decelerations in the event of a fall that could have been substantially greater than those a galloping rhinoceros risks.
Two-Stage, Variable skid Distance Model —Several scenarios based on predictions of this model are summarized in Table 4 View TABLE 4 . It is important to note that, for a horizontal speed of 10 m/s at the time the dinosaur stumbles, the torso of a falling Tyrannosaurus would experience the injurious horizontal forces of the slide for a total distance of only 1.8 meters, only Vs the total distance of the slide for the same animal running at 20 m/s. Thus any damaging effects of sliding on the ground should increase dramatically with increasing sprint speed.
Calculations for the torso of a white rhinoceros that falls while running at 7.5 m/s yield decelerations and forces about 1/2 as large, and a skid distance about 1/12 as far, as experienced by a Tyrannosaurus running at 20 m/s.
It is interesting to note that the “high-g” initial slide distance d1 does not vary greatly across the torso scenarios in Table 4 View TABLE 4 , remaining roughly in the range 1-2 m. Furthermore, from 50% to 90% of the initial kinetic energy is dissipated (force x distance), and hence most of the damage occurs, during the high-g skid phase. This may be verified by noting that the work done by friction at the expense of kinetic energy is
W1 = Fhld 1, and W2 = Fh2d2,
in the high-g and low-g phases, respectively. The sum W1 + W2 equals the initial kinetic energy. For example, for the torso of Tyrannosaurus running at 10 m/s the ratio W1/(W1 + W2) equals 0.85, or 85%. These observations provide some rationale for the much simpler fixed skid distance model (which corresponds roughly to d1 in the more elaborate two-stage fall model).
Note, too, that for a Tyrannosaurus running at 20 m/s when it trips, the total skid distance of the torso exceeds that of the head by 3 meters ( Table 4 View TABLE 4 ). In this model, the torso overtakes the head near the end of the slide—the dinosaur might literally break its neck!
In order to model kinder and gentler falls, we have carried out calculations in which either the squash distance delta y or the hole depth h2 is doubled for each scenario in Table 4 View TABLE 4 . The vertical and horizontal accelerations and forces decrease by 20%-30%, but the “high-g” slide distances increase by 10%-80%. Thus the decrease in damaging “high-g” forces is offset by
the increased distance over which these forces are applied. How much this enhances the survivability of the fall is consequently problematical.
The numerical results of our two-stage model differ somewhat from those obtained from our much simpler model with a fixed skid distance of 3 m, but the conclusions remain the same. Even though the two models of the horizontal deceleration experienced by a Tyrannosaurus unlucky enough to fall while sprinting at a high speed are quite different, both suggest that the consequences of the fall would be drastic.
The Risk of a Fall: Conclusions— Based on our models of the vertical and horizontal forces and decelerations of a fall, it seems safe to say that, if a 6,000-kg Tyrannosaurus were to fall while running at 20 m/s, its chances of survival would not be good. Even discounting the threat of death, we suspect that an animal would be cautious about engaging in any activity that might entail a significant risk of non-lethal injury that would hamper its ability to obtain food or carry out other activities necessary for survival. Even if the dinosaur were structurally able to achieve speeds of 20 m/s—a conclusion that seems unlikely, given the values of the strength indicator for Tyrannosaurus obtained by Alexander (1985, 1985) and by us—we doubt that the benefits of moving at this speed would outweigh the attendant risks.
CONCLUSIONS
We think that Tyrannosaurus was an active animal for its size, and we concur with Holtz (1994) that it probably was capable of attaining faster speeds than equally large theropods of other clades. However, our estimate of the strength indicator of Tyrannosaurus , taken in conjunction with the decline in locomotor performance likely to occur in very large animals ( Garland, 1983; Biewener, 1989a, b; Chappell, 1989; Bertram and Biewener, 1990), structural features of the hind limb and the hip joint of Tyrannosaurus , and the dire consequences likely to afflict a 6000-kg animal that falls while running, lead us, like Alexander (1985, 1989), to doubt that Tyrannosaurus was as fleet as fast modem cursors. We also doubt, like Gatesy (1991), that adult individuals of Tyrannosaurus (our conclusions do not necessarily apply to juveniles) could run as rapidly as other, smaller theropods, such as omithomimosaurs, or even smaller-bodied tyrannosaurs like Albertosaurus (cf. Holtz, 1994).
We doubt that adult individuals of Tyrannosaurus ran with a long suspended phase, in which both feet were simultaneously off the ground for a significant interval of time during a stride (cf. Thulbom, 1982, 1990). On the other hand, even though Tyrannosaurus had a lower strength indicator than Ceratotherium , the dinosaur, because of its long legs, might have been able to exceed the white rhinoceros’ 7.5 m/s (cf. Bakker, 1986) without a long suspended phase, by moving at a fast walk, or possibly even a trot. Although we cannot with certainty say what the top speed of Tyrannosaurus rex was, 10 m/s would not surprise us, and even 15 m/s might have been possible. A top speed of 20 m/s seems very unlikely. Our guesses about the sprint speed of Tyrannosaurus are greater than that of Thulbom (1982, 1990), but less than those of Bakker (1986) and Paul (1988).
Interestingly enough, our estimate of the top speed of Tyrannosaurus is similar to that predicted for a 6,000-kg mammal by the change-point, segmented regression model of Chappell (1989). It is also similar to the sprint speed of the African elephant (Loxodonta africana) cited by Garland and Janis (1993); the femur of the African elephant has a strength indicator very close to the values we obtained for Tyrannosaurus (Alexander, 1985, 1989).
Our conclusions about the cursorial potential of Tyrannosaurus are consistent with the presently-known trackway record of bipedal dinosaurs ( Farlow, 1987; Molnar and Farlow, 1990; Thulbom, 1990), although possible artifacts in the ichnological record (Molnar and Farlow, 1990) mean that dinosaur tracks do not unambiguously argue against rapid locomotion in very large theropods. In any event, our conclusions are, at least in principle, readily falsifiable. All it would take is a single trackway of a T. rex-sized theropod in which the stride length is large enough to indicate a very rapid running speed. Alexander’s (1976) formula for estimating speeds from trackways can be rearranged to show that, in order to have been running at 20 m/s, Tyrannosaurus (with a hip height of about 3 meters [Thulbom, 1990]) would have had a stride of about 15 meters.
Finally, given the likely consequences of a fall, we suspect that Tyrannosaurus was very careful about the circumstances under which it chose to move at its top speed, whatever that speed was.
TABLE 1. Selected measurements of a full-sized Tyrannosaurus rex, based on Matt B. Smith’s model restoration. The model’s scale is 1/20.
| Total length of the animal, snout to tailtip, measured along the curve of the dinosaur’s back—1,196 cm |
|---|
| Head length— 162 cm |
| Neck length —120 cm |
| Body length from in front of the shoulder to the back of the hip—320 cm |
| Tail length—594 cm |
| Height of the top of the head above the ground—460 cm |
| Height of the lower edge of the lower jaw above the ground—346 cm |
| Height of the top of the hip above the ground—356 cm |
| Height of the lowest spot on the belly (at distal end of pubis) above the ground—146 cm |
| Maximum dorso-ventral body depth—208 cm |
| Maximum width across hips—96 cm |
| Maximum chest width—98 cm |
TABLE 3. Mass estimates of Tyrannosaurus rex.
| Estimated mass (kg) | Source of data |
|---|---|
| 3,000 + | Bakker (1986) |
| 3,244 | Campbell and Marcus (1992) |
| 4,500 | Anderson et al. (1985) |
| 5,400-6,300 | This study |
| 6,890 | Colbert (1962) |
| 7,400 | Alexander (1985) |
| 7,700 | Colbert (1962), as modified by |
| Alexander (1989) | |
| 5,700-12,000 or more | Paul (1988) |
TABLE 4. Horizontal accelerations (ah), forces (Fh), and slide distances (d) ofa falling Tyrannosaurus or Ceratotherium (white rhinoceros) with various running speeds (Vo) at the time the fall begins. The coefficient of kinetic friction цk is assumed to be 0.8. The subscripts 1 and 2 refer to the initial “high-g” slide phase and the final slide phase, respectively. The total slide distance is d, and d' is the total slide distance neglecting the “high-g” slide phase. Forces are in newtons (N), accelerations are multiples of the gravitational constant g, and slide distances are in meters (m).
| Scenario | a hl (g) | a h2 (g) | Fh1 (N) | Fh 2 (N) | d1 (m) | d2 (m) | d (m) | d' (m) | |
|---|---|---|---|---|---|---|---|---|---|
| Tyrannosaurus torso (Vo = 20 m/s) | 5.4 | 0.8 | 2.4 x 105 | 3.5 x | 104 | 1.9 | 12.4 | 14 | 26 |
| Tyrannosaurus head (Vo = 20 m/s) | 12.4 | 0.8 | 8.4 x 104 | 5.4 x | 103 | 1.0 | 9.9 | 11 | 26 |
| Tyrannosaurus torso (Vo = 10 m/s) | 5.4 | 0.8 | 2.4 x 105 | 3.5 x | 104 | 0.80 | 1.0 | 1.8 | 6.4 |
| Tyrannosaurus head (Vo = 10 m/s) | 12.4 | 0.8 | 8.4 x 104 | 5.4 x | 103 | 0.39 | 0.38 | 0.77 | 6.4 |
| Ceratotherium torso (Vo = 7.5 m/s) | 2.9 | 0.8 | 8.6 x 104 | 2.4 x | 104 | 0.92 | 0.24 | 1.2 | 3.6 |
No known copyright restrictions apply. See Agosti, D., Egloff, W., 2009. Taxonomic information exchange and copyright: the Plazi approach. BMC Research Notes 2009, 2:53 for further explanation.
|
Kingdom |
|
|
Phylum |
|
|
Class |
|
|
Order |
|
|
Family |
|
|
Genus |